If you’ve spent any time following professional cycling and the exploits of the world’s best climbers (including those with chequered pasts), you would probably have heard of power-to-weight ratios. Expressed as watts per kilogram, these numbers are often used when talking about how fast a rider climbed a particular hill.
So what exactly are power-to-weight ratios, what are they good for, and how are they relevant to everyday riders like you and me?
Quite simply, power-to-weight ratios are the amount of power a rider is able to push through the pedals divided by the rider’s weight (excluding the weight of their bike and anything they’re carrying). What these ratios allow us to do is compare the performance of riders of different weights and who are able to produce different amounts of power.
Different weights, same power output
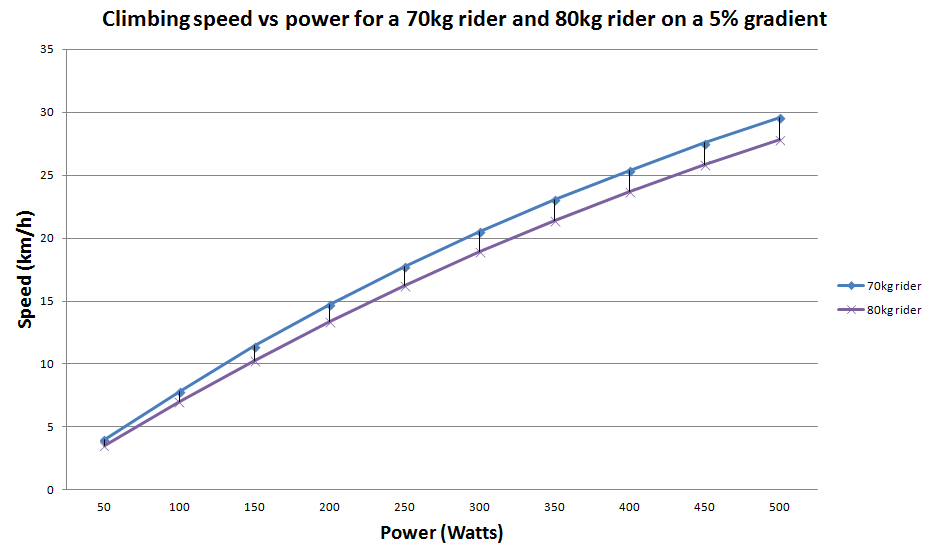
You might recall from the last article the example of two riders who have different weights but are both able to produce the same amount of power. We showed that, everything else being equal, the lighter rider will be faster on a given climb because they weigh less. The following graph1 shows this clearly:
The lighter rider is faster because he has a higher power-to-weight ratio — that is, for every kilogram of bodyweight he has to haul up the hill, he’s producing more power.
To understand why a higher power-to-weight ratio means a faster climber, consider this complicated-looking but actually quite simple formula we introduced in the previous article:
P = krMs + kaAsv2d+ giMs
You can see what each of the terms means in the previous post, but essentially, the power required to climb at a certain speed equals the power required to overcome the rolling resistance of the road (krMs) plus the power required to overcome the wind resistance (kaAsv2d) plus the power required to overcome the gradient of the hill (giMs).
That final term in the equation — the one relating to the hill’s gradient — scales according to the rider’s mass. The heavier the rider, the more power required to overcome the gravitational force pushing them down the hill. The lighter rider, by contrast, needs to produce less power to stay with his or her heavier mate … or if they can produce the same power, they’ll be able to climb noticeably faster.
The effect of gradient
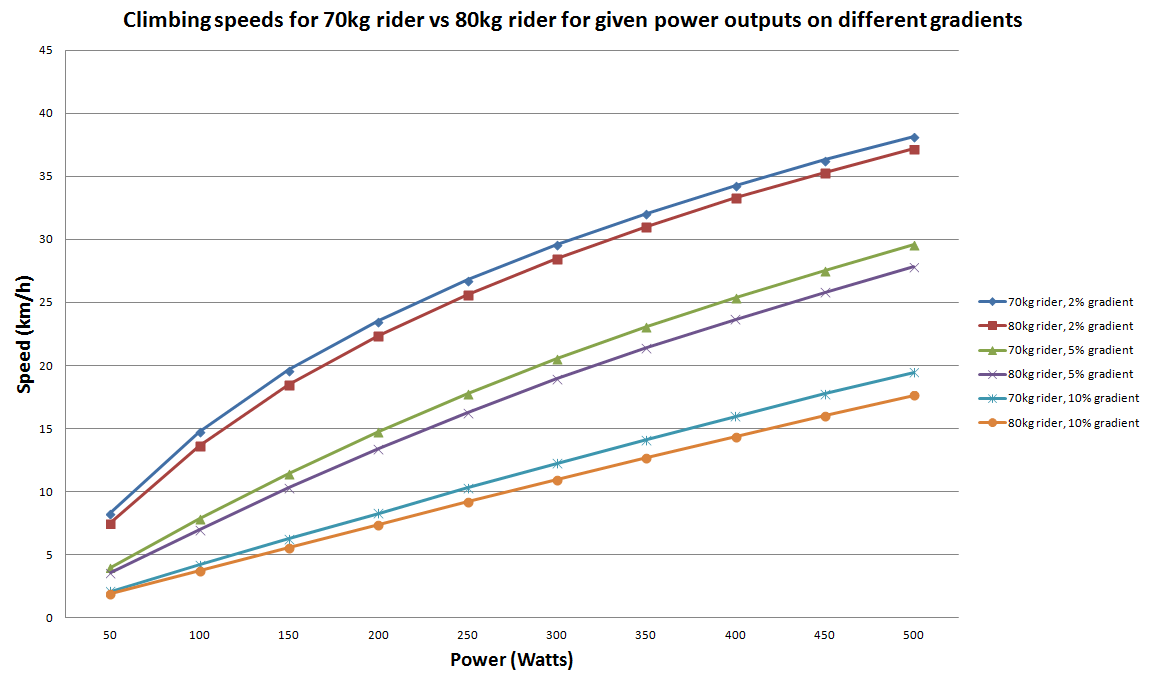
If you’ve done a bit of climbing in the past, or if you’ve watched much bike racing on TV, you’ll know that the steeper the road, the greater advantage lighter riders seem to have. Here’s a graph showing how fast our 70kg rider and our 80kg rider can climb on different gradients, assuming they’re both putting down the same amount of power.
The top two lines show the riders’ speeds on a 2% gradient, the middle two lines show their speed on a 5% gradient, and the bottom two lines show how fast they could ride on a 10% gradient.
You’ll notice that as the gradient increases, the difference between the riders’ speed increases. Why is this?
Well, let’s consider our formula once more; the one with the three components. The power needed to overcome rolling resistance will stay the same as the gradient increases but the power needed to account for the wind resistance and gradient components will both change.
The wind resistance component scales according to the rider’s speed cubed — that is, as the speed increases, the wind resistance increases dramatically. But as the rider’s speed decreases (as a result of going uphill), the power required to overcome wind resistance also decreases.
This is why you don’t get as much of an advantage slipstreaming your mates on a climb — there’s less of a saving to be had by sitting out of the wind when the speed is low. This is also why steeper gradients favour lighter riders — with the diminished wind resistance, it’s the gradient component that makes up the bulk of the power needed to travel at a certain speed. And because that part of the equation factors in the rider’s weight — as discussed above — the lower the weight, the lower the required power to climb at a certain speed.
Different weight, same power-to-weight ratio
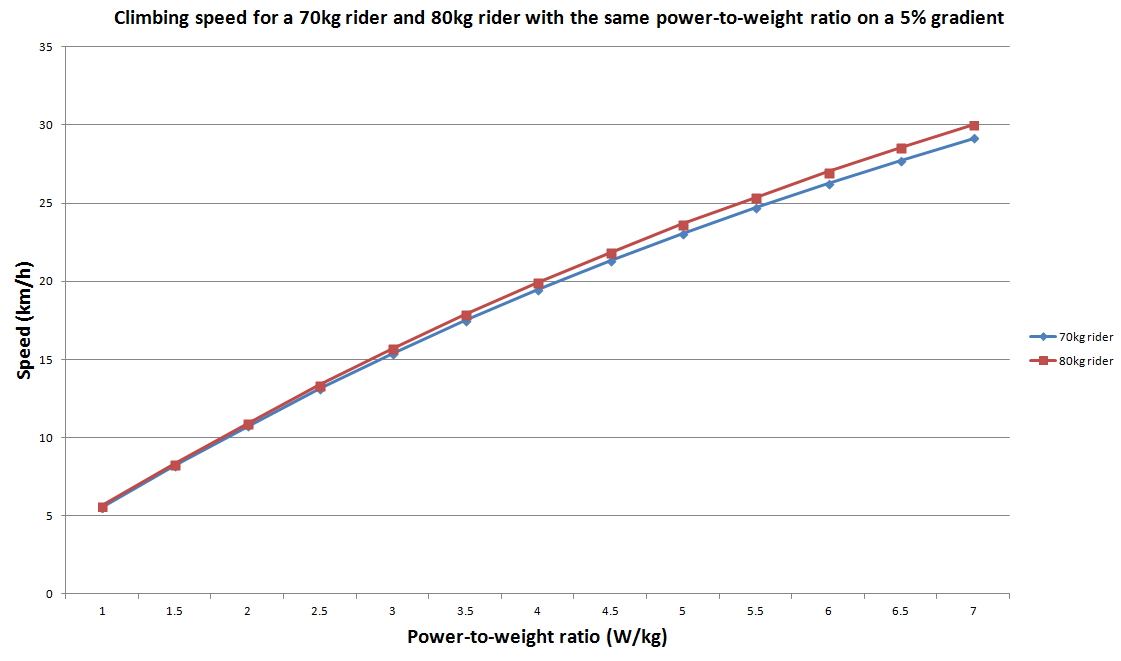
So we know that if a 70kg rider and an 80kg rider are producing the same amount of power the lighter rider will climb faster. But what if the heavier rider is producing more power than the lighter rider and the two have the same power-to-weight ratio? Well, you get a graph that looks something like this:
As you can see, two riders with the same power-to-weight ratio (even though they are producing different amounts of power) will climb at close to the same speed (assuming everything else is equal).
You’ll notice that at higher power-to-weight ratios the heavier rider starts to get a bit of an advantage. The reason for this can be seen by referring, once again, to the formula above.
As a rider’s speed increases, so does the wind resistance acting on the rider and therefore the amount of power required to overcome that wind resistance. As a result, the higher the speed, the greater the advantage a more powerful rider will have.
It’s worth noting, however, that in the real world, more powerful riders also tend to have a greater “frontal area” (the A in kaAsv2d). This means that the power required to overcome wind resistance increases again as the size of the rider increases, which reduces the advantage of being able to produce more power.
Power-to-weight ratios for the average rider
So how does this discussion of power-to-weight ratios affect us everyday riders? Well, it’s as simple as this: if you want to climb faster, you need to improve your power-to-weight ratio. There are three ways you can do that: lose weight, improve your power output or, even better, lose weight and improve your power output.
A discussion about weight loss for cyclists is beyond the scope of this discussion but this article from CyclingTips and this piece about my own attempts at weight loss might be of interest. In terms of improving your own power output, your best bet is to get a powermeter to allow you to see what sort of power you’re producing now and track your performance as you improve.
While powermeters were once too expensive for most recreational cyclists to consider buying, the introduction of products like Garmin’s Vector pedals and the Stages crank-based powermeter (which I use and love) have made tracking your power more affordable than ever before. If a powermeter is still out of your reach, consider visiting a spin studio that uses a WattBike or other machine that can measure power output.
There are a handful of ‘popular’ intervals that you can do to give you a baseline measurement of where you’re at: a five-second sprint effort, a one-minute effort, a five-minute effort and a 20-minute effort, the last of which you can use to work out your threshold power (your best effort over one hour). Here’s Dan Lloyd from the Global Cycling Network with a good explanation of each test and how you can do them.
If you’re the sort of rider that enjoys racing, or you’re just curious to see how you stack up against others, you might want to check out this popular power table by Andy Coggan. It provides a handy reference for the power-to-weight ratios you’re likely to come up against at various levels of competition.
You might notice that you’re stronger at one interval than another, which is totally normal. You might also notice that the pros have power-to-weight ratios that are simply unfathomable for us mere mortals. The trick is to use this as inspiration, rather than letting it get you down!
With a baseline figure for your power-to-weight ratios you’re now ready to start improving. Tips on how to get those power numbers up are also beyond the scope of this article but these articles from CyclingTips should get you on the right track.

To wrap things up, power-to-weight ratios might be a simple concept but they’re a powerful measure of climbing performance and how we stack up against others. Delving into the basic science behind these ratios provides a welcome reminder of the two main levers in our control when trying to improve our climbing speed: power output and weight.
The exciting thing is that, for most of us recreational cyclists, there’s plenty of room to improve in both areas. Sure, we all reach a genetic ceiling at some point — and some people are blessed with “better” genes than others — but if you’re interested in improving your climbing there’s plenty you can do.
In the next instalment in this series we’ll talk about VAM, what it is, and how it can be used to help you estimate (and therefore improve) your climbing performance.
Footnotes:
1. The data points in this graph were generated using the Bike Calculator website. Both riders were on a 9kg bike, riding on the hoods, using clincher tyres, at an elevation of 100m, at 25 degrees celcius and with no wind around.








very clear and good article easy to understand. Thank you
Good thing I didn’t read this until today. I have mathematical proof that the Fitz’s 105 I finished yesterday was impossible, which would have been bad for morale.
I might be able to help with a guide to the ideal weight (range) for cycling. http://templeblot.wordpress.com/2013/12/10/calculating-the-ideal-weight-for-cycling/
Yet the really fascinating part is why doesn’t a sprinters power watts/kg translate to a fast time up a climb? We know that a rider like Cancellara can generate excellent power to weight ratios and watts output, yet he can’t match it with a typical climber like Froome for example – whereas in a time trail the climber can’t match it with Cancellara even though the climbers watts/kg would be superior …… wouldn’t it?
So there’s something missing in this science of climbing. As raw power figures should suggest that Cancellara would be able to climb nearly as quick as the climber as he has the power to weight ratio – watts output. There must be other variables or qualities that a climber has vs what a time trial, etc rider has – what is it? Fast vs slow twitch? Maybe? Vo2 would be similar, its something that needs to be addresses beyond more simple analysis. Sagan would be a good example.
What is missing is the differing effects of gravity as gradient increases. I’m not sure if this is mentioned or not actually – I only skimmed the article – but, suppose 2 riders have the same power to weight ratio – I’ll use 6.2 w/kg as it makes it a real life example (both pro riders), but they have different weights; one is 63kg and one is 76kg. So, doing a bit of arithmetic, the 20 minute power of one is about 390 and the other is about 470 (a national TT champ). If the hill is 1% the 470 watts is going to win. The same at 2% 3% 4% et cetera, until the road reaches a certain gradient – and, at that point, they will be level. The exact gradient must depend on the 2 individuals being compared. At steeper gradients the lighter rider will start to have an advantage. At 25% the advantage will be very obvious. This is because more and more force is required to move the heavier rider against gravity as the gradient gets closer to vertical.
I had the same question and found a good article explaining it:
https://cyclingtips.com/2013/09/climbing-and-time-trialling-how-power-outputs-are-affected/
Great article. Is there any formula to determine why I’m such a shit rider?!
Good article. But it calls 7 bogus and refers to sassi’s 6.2 as a more realistic upper ceiling . Dumoulin’s vuelta data had no 30min effort better than 5.9.
After a lazy winter I’m seeing how much slower you get losing 30w and gaining 5 or 6 kgs
What I find most phenomenal is how hard it is to get to those professional power to weight numbers. You need to be able to sustain over 5w/kg to be competitive in B grade Victorian Road Series races, and yet “only” another ~1.5w/kg gets you to World Tour levels.
Ahh, but thats only 1.5w/kg after 4-5 hours of racing for 3 weeks straight 🙂
aside from the obvious speculation on how, from what I’ve read on training, the way to get your power-weight up that high is just very intense training. while amateurs train pretty hard, and it’s hard to imagine training that much harder, this is what pros can do – by virtue of massive km in their legs. doing 30,000km a year for consecutive years gives you that stamina to tolerate harder training. this is what I’ve read about the East German model, where their team pursuit riders just rode massive km at mostly moderate intensity, to build their bodies up for a short period of intense training that gave them their top end power.
Don’t mistake intensity for volume.
I agree about is that the intensity can only be performed on a base of cardiovascular fitness. That’s what the volume is for.
But the greatest mistake many folks make is trying to train too hard for too long. The result, in practice, is training quite hard for quite long. This is not useful for race conditioning.
In my experience (and I have been lucky enough to train alongside national champions and stage race winners) road pros do their volume training shockingly easy, and their hard efforts are very, very intense indeed. It seems the middle ground is a waste of time. Sadly most bunch rides occupy that middle ground and are rotten training as a result.
The other huge mistake many amateurs make is insufficient recovery. There’s little value in doing repeats of that ten-minute hill effort when your capability is blunted by long-term fatigue, and we all know that the body adapts after the effort, not during it.
That’s very old school training philosophy…and it hides a lot of inefficiency and physiological ignorance. That training burns out 9,996 riders out of 10,000. It can also shorten the remaining 4’s competitive careers.
It’s way smarter to ensure an athlete is not at any stage overtraining, for this is when the body breaks down, and the opposite effect results. Overtraining does not toughen the body. It results in poorer sleep, recovery, and muscle adaptation…and more scarred muscle. It can also exhaust endocrine systems (adrenal glands, pancreas, thyroid, pituitary) which all impact endurance. Further, sprint speed is in no way developed by endurance training.
By far the most advanced way to train is to use power meters to ensure one is pushing to up to the point of burn out, but staying just short of it. Newer methods also use periodization more so, because it’s shown that some stress is cumulative, and having 4 or more weeks easing off top intensity training assists better adaptation. This is even more relevant for Masters athletes who do not adapt to training stimulus as significantly, and do not recover as well.
going from 5w.kg to 6.5w.kg in is 30%!! for a 60kg rider that’s going from averaging 300watts for 20 minutes to averaging 390 watts, which is significant 🙂
I found this useful in trying to lose weight
http://www.53×12.com/do/show?page=article&id=3
The key part of power-to-weight in top level stage racing is what is produced by a rider over the bigger climbs. The part that I find most interesting is the actual human physiological limits that are possible once the climb length goes over 30 minutes; typically, 7 w/kg is looked at as being the maximum sustainable, and that beyond that figure, there’s likely to be something unusual going on. Of course, without having specific power and weight details, people are (educatedly) guessing as to what the w/kg is for a given climb.
There’s some interesting info at http://sportsscientists.com/2010/07/cycling-performance-what-is-possible/ that goes into how w/kg relates to VO2 max and that physical limit.
@marcus – 7w/kg for 30 minutes and something unusual is already going on!!
Indeed, I should have clarified it as a ‘theoretical’ maximum – even the article I linked to talks about Riis’ 6.8 and Armstrong’s 6.6 efforts for 35/38 minutes being beyond believable, and Aldo Sassi talking about 6.2 being indicative of doping. I should have linked to the article I took that number from at the time because I can’t find it now :D. Aside from that, I find using 7w/kg is a clear definitive point of reference; if people haven’t read into it enough, or understand the difference between a 20min and 60 min effort, taking into account weather, stage length, timing of the stage, etc etc, the relative difference of someone riding at 5.8 or 6.2 becomes more of a ‘it all depends’.
Contador’s 2009 ride up Verbier is a good example of one of those rides on the limit of possibility and belief – http://sportsscientists.com/2009/07/tour-de-france-2009-contador-vo2max/