A quick note: the formula used in this piece might look a little daunting but it’s a lot simpler than it seems.
There are a number of ways of objectively measuring the difficulty of one gradient compared with another. For a start we need to realise that there are three main forces acting against a cyclist while riding: wind resistance, road friction and gravity. These three forces can be represented in the following formula¹:
P = krMs + kaAsv2d+ giMs
where
- P = power required (in watts)
- kr= rolling resistance coefficient
- M = mass of bike + rider
- s = speed of the bike on the road
- ka= wind resistance coefficient
- A = the frontal area of the bike and rider
- v = speed of the bike through the air (i.e. bike speed + headwind or – tailwind)
- d = air density
- g = gravitational constant
- i = gradient (an approximation²)
To help understand that jumble of letters above, it helps to realise that the equation can be broken down into three parts. In simple English: The total power required = the power required to overcome rolling resistance + the power required to overcome wind resistance + the power required to overcome the gradient.
Let’s assume I want to work out how much power (in watts) I need to produce to get up a hill of 5% gradient at a speed of 10km/h (not very fast). The values I need are:
- kr= rolling resistance coefficient = 0.005 (for a typical bitumen road on clinchers3)
- M = mass of bike + rider = 90kg (my bike’s a little heavy)
- s = speed of the bike on the road = 2.78m/s (i.e. 10km/h)
- ka = wind resistance coefficient = 0.5 (no headwind or tailwind)
- A = the frontal area of the bike and rider = 0.6m² (climbing on the bar tops)
- v = speed of the bike through the air = 2.78m/s (no wind)
- d = air density = 1.226kg/m³ (at roughly sea level)
- g = gravitational constant = 9.8m/sec²
- i = gradient = 0.05
You’ll recall that the formula looks like this:
P = krMs + kaAsv2d + giMs
So plugging in the various values we get:
P = (0.005 x 90 x 2.78) + (0.5 x 0.6 x 2.78 x 2.78² x 1.226) + (9.8 x 0.05 x 90 x 2.78)
P = 1 + 8 + 123
P = 132W
Note how little power is required to overcome rolling resistance (1W) and wind resistance (8W) compared with gravity (123W).
While I’d need to deliver 132W to the back wheel in order to keep moving at 10km/h, the road bike isn’t a perfect machine and the power I push through the pedals isn’t the same amount that’s delivered to the wheel. We can estimate that a well-maintained bike has a drivetrain efficiency of roughly 95% though, so:
132W /(95/100) = 139W
So, at 90kg (me + my bike), on a hill of 5% gradient, with no wind and on a decent road surface, I need to produce roughly 139W of power to travel at 10km/h. Easy.

What about if I wanted to average 20km/h (5.55m/s) up the 5% hill in the example above? Well, we just replace 2.78 with 5.55 in the formula above to get:
P = (0.005 x 90 x 5.55) + (0.5 x 0.6 x 5.55 x 5.55² x 1.226) + (9.8 x 0.05 x 90 x 5.55)
P = 2 + 63 + 245
P = 310W
Accounting for drivetrain efficiency of 95%, I’d actually need to produce 326W to travel at 20km/h up the hill.
You can see that the power required to overcome the rolling resistance at the increased speed is still tiny (2W), but the wind resistance has increased dramatically4 (63W). And of course, the power required to overcome the 5% gradient at a higher speed is much higher.
So, how does the required power change depending on the gradient, assuming we’re talking about a constant speed? That is, objectively, how much harder is one gradient compared to another?
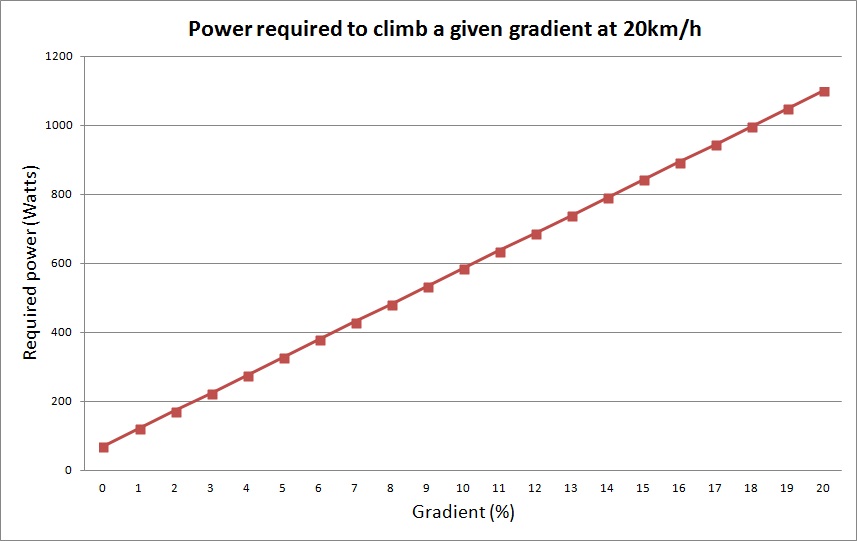
I’ve gone through and calculated the required wattage for the whole number gradients from 0% (a flat road) to 20% (ouch), assuming that I want to maintain a speed of 20km/h on each of those grades. I’ve also factored in drivetrain efficiency. Here’s a graph:
As you can see, the line of best fit is straight, meaning the required power increases proportionally with the gradient of the hill. So, at 90kg (rider + bike), and with the assumptions made above5, I need to produce roughly an extra 52W of power for every percentage point the gradient increases by, in order to maintain 20km/h. This number will be different for every rider, and depends on many factors.
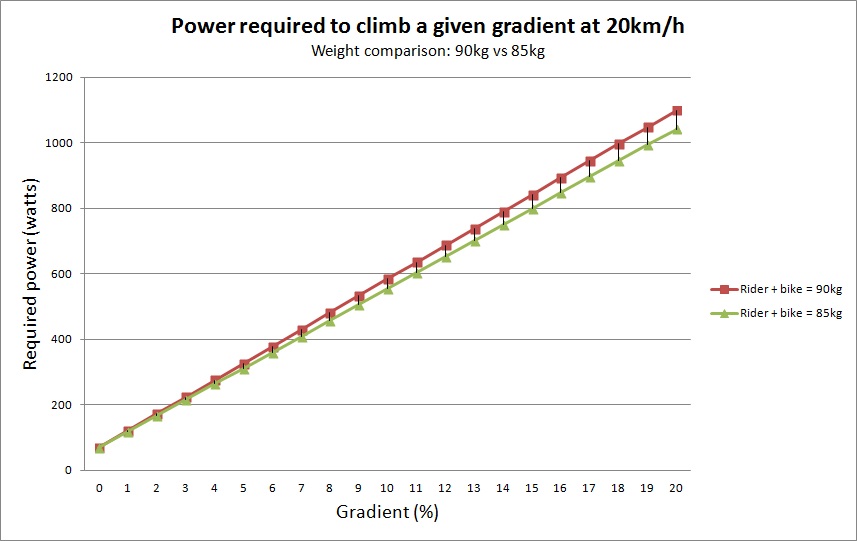
One of the biggest factors, of course, is weight. If you’re lighter, you’ve got less mass to haul uphill and therefore less power required to ride at the target speed. That’s why the best climbers in the world are super light (while still able to maintain a high power output).
To emphasise this point, here’s the above graph with an extra line added to represent a rider and bike with a combined weight of 85kg (i.e. what would happen if I lost 5kg):
It mightn’t seem like there’s much of a difference, particularly at lower gradients, but every watt counts, especially on a long ride with lots of climbing, like the 3 Peaks Challenge. If you have to push a few extra watts uphill every time you climb, this can make a significant difference to your fatigue levels by the time you reach the final climb.
Of course, a difference of just a few watts can make a massive difference in a race situation too, or even if you’re just trying to beat your mates up a hill. Let’s use arguably the most well-known climb in Melbourne, the 1 in 20, as an example.
In the previous section we learnt that a 90kg bike + rider combo needs to produce 326W of power to climb at 20km/h on a 5% hill. Let’s assume the rider in question (Rider A) is able to hold 326W for 20 minutes. Rider A’s mate, Rider B, is also able to hold 326W for 20 minutes, but he and his bike combined only weigh 85kg. Both riders head out to the 1 in 20 to see who can get to the top of the climb first.
It’s pretty obvious at this point that Rider B is going to win, all things being equal, but by how much? Let’s take the formula we used above and reverse-engineer it:
P = krMs + kaAsv2d + giMs
You’ll recall that 326W is the required wattage when considering a drivetrain efficiency of 95%, which correlates with 310W on the road — the power we need to use in this calculation. For this calculation we’ll also need the average gradient of the 1 in 20 which is more or less 4% (not 5% as the climb’s name would suggest).
So, for Rider A:
310 = (0.005 x 90 x s) + (0.5 x 0.6 x s x v² x 1.226) + (9.8 x 0.04 x 90 x s)
Now let’s assume that v and s are the same value — that is, that there’s no wind to speak of:
310 = (0.005 x 90 x s) + (0.5 x 0.6 x s x s² x 1.226) + (9.8 x 0.04 x 90 x s)
310 = 0.45s + 0.37s³ + 35.28s
310 =35.73s + 0.37s³
Solving the equation from here isn’t trivial but with the help of an online “cubic equation calculator” I can tell you that s = 6.20m/s or 22.3km/h.
At this average speed, how long would the 6.8km-long climb take?
(6.8/22.3) x 60 = 18.3 minutes = 18 minutes 18 seconds
And what about Rider B, who’s just as powerful as rider B, but 5kg lighter?
310 = (0.005 x 85 x s) + (0.5 x 0.6 x s x v² x 1.226) + (9.8 x 0.04 x 85 x s)
Again, let’s assume there’s no wind about:
310 = (0.005 x 85 x s) + (0.5 x 0.6 x s x s² x 1.226) + (9.8 x 0.04 x 85 x s)
310 = 0.43s + 0.37s³ + 33.32s
310 = 33.75s + 0.37s³
Using our cubic equation calculator we find that s= 6.36m/s or 22.9km/h.
And how long will that average speed take Rider B to finish the climb?
(6.8/22.9) x 60 = 17.8 minutes = 17 minutes 48 seconds
So Rider B wins by 30 seconds. It’s worth noting here that the 1 in 20 probably isn’t the best hill to use as an example as there are two significant gradient changes: from the first section into the false-flat, and from the false-flat into the final section of the climb.
Breaking the 1 in 20 down into three sections — 3.3km at 4.5%, 1.1km at 1.9% and 2.4km at 4.5% — and running the calculations again returns a slightly different result: 17 minutes 30 seconds versus 18 minutes 7 seconds. But this example should make it clear that the lighter you are the better suited you are to climbing, assuming a fixed power output.

Here’s another way of looking at it.
A typical masters C-grade rider might be able to sustain 300W for an hour, but above this “functional threshold power”, his endurance will drop off quickly. He might be able to push 330W for 15 minutes, for example, but as the wattage increases, the length of time he’s able to maintain that wattage for decreases.
Now let’s assume this C-grade rider is racing in a bunch when the riders turn a corner and start climbing. Let’s say that our rider needs to climb at about 25km/h in order to stay with the bunch up the climb and that maintaining that speed requires our rider to produce 330W.
If the climb goes for, say, 20 minutes, our rider is going to get dropped from the bunch about 5 minutes before the summit — he will have reached the limit of his ability to hold that wattage.
Now imagine if the same rider, with the same functional threshold, managed to lose 5kg. The power he’d need to produce in order to climb at 25km/h would now be noticeably less than 330W. As a result our rider might be able to stay with the bunch for the entire 20-minute climb.
This issue of power-to-weight ratios deserves an article (or several) of its own, but we can see from the above that there are three main ways you can improve your climbing speed:
- Lose weight — you won’t need to produce as much power to haul yourself and your bike uphill
- Increase the amount of power you can produce
- Both
If you’d like to have a play around with some numbers yourself, without having to worry about formulas, variables and coefficients, I’d highly recommend the Bike Calculator website and the excellent and free Bike Calculator app for iDevices.
Thanks very much for reading.

Footnotes:
- The formula used in this article is derived from the formula discussed here, albeit with the inclusion of air density in the wind resistance calculation, as per here.
- For the sake of approximation, we can use the climb’s percentage gradient/100 for the variable “i” in this equation. That is, a gradient of 5% can be plugged in as 0.05. Technically, the value should be the sine of the angle of the slope in degrees. For example, a 5% hill has an angle of 2.86º, and sin(2.86º) = 0.049 which is close enough to 0.05. Even at very steep gradients, the percentage gradient/100 approximation is fine (e.g. 20% = 11.31º. sin(11.31º) = 0.196)
- Riding on heavier, wider tyres and/or riding on rough roads will increase the rolling resistance coefficient, meaning you’ll have to produce more power than you would on a smoother road, with thin tyres, for a given speed. See here for more information.
- The power required to overcome air resistance is proportional to the speed of the bike cubed (assuming there’s no wind).
- Rolling resistance coefficient = 0.005, frontal area = 0.6m², air density = 1.226kg/m³.






very clear and good article easy to understand. Thank you
Hi everyone,
Hope you are doing well and staying safe.
I have a Wahoo Kickr Core which can simulate gradients up to 16% and I am using it with Rouvy which is always at 100% in TT mode. My bike is a Specialized Tarmac SL6 with 11sp – 11-28T on the trainer.
I have been training on a local mountain indoor – however I note that the incline of the mountain at some points are above 25%. Given that the Kickr Core simulates only up to 16% – I am wondering whether I could use my gears to add the additional 9%.
So – in my mind – it works like the below examples:
on gradients of 11% – the Kickr Core will simulate 11% at 100% using Rouvy TT Mode – so when I am on my easiest gear – 34T & 28T – I am getting 11% of incline simulation
on gradients of 16% – the Kickr Core will simulate 16% at 100% using Rouvy TT Mode – so when I am on my easiest gear – 34T & 28T – I am getting 16% of incline simulation
However,
on gradients of 25% – the Kickr Core will only simulate 16% at 100% using Rouvy TT Mode – so when I am on my easiest gear – 34T & 28T – I am only getting 16% of incline simulation
What happens if I am on a gradient of 25% – I change gear to 34T & 25T – would this add to the 16% simulated by the Kickr Core?
If yes then how much more gradient would I add on the 16% gradient simulated by the Kickr Core just by shifting to 25T?
If I shift to the hardest gear – 11T – would that simulate even more gradient on top of the 16% by the Kickr Core? Is there a way to know how much more gradient it will add?
If my understanding is wrong – can you guys please explain why?
Thank you
This was a great read and I learned a bunch..but I was just looking for what setting on my peloton to kinda simulate a 10% grad..
In your formula a lower air density (like you have in higher altitudes) means less effort, is that correct? That would mean it becomes more easy to climb at 1.500m vs. sea level.
True, air density at 1500 m is approximately 85% of that at sea level, so going back to the 90 kg rider + bike traveling 20 km/h up a 5% gradient, the power to overcome drag drops from 63 W to 54 W, bringing total power down from 310 W to 301 W. Not really that much savings, especially considering the decrease in oxygen content at altitude.
Yes, but your ability to take in enough oxygen also decreases as the altitude increases! So your ability to maintain the required power starts to fade…. This starts to kick in above 1500m or so. Above 2500m it becomes very noticeable.
Could someone explain this in terms of energy instead of power? For example, what’s the difference in calories burned when ascending a hill with 1km elevation as opposed to riding an equivalent distance over a flat surface? I’m curious how much more energy hill climbing burns as opposed to flat routes.
The maths is pretty simple, actually. Energy = power x time (or integral P(t)dt if your power isn’t constant) and energy is also force x distance (same story with the calculus). Provided you also know how fast the bike is going, you can use either one of these formulas. With the force x distance calculation, you have to take into account the length of the slope, which is basically the hypotenuse.
If your climb has flat sections, you will have to calculate the energy for each section separately and sum them.
To compute the energy, the only part that you need to sum (or integrate) is the air-resistance term. Both the rolling friction term and term corresponding to climbing depend only on total distance you have travelled, and total distance you climb, respectively (ignoring the possibility of down-hill sections, which you can ignore if you do not pedal)
I think you may have missed a factor of g in the rolling resistance term. Most other expressions found while googling have an extra g product with similar values for the coefficient as you have here. I require a lot more than 2 watts to propel my bike at 20km/h on a flat road even in a vacuum 🙂
Your formula states: Power required to overcome rolling resistance, P = krMs. Mass times speed is (kg)*(m/s), which does not produce Watts. W = (kg*m^2)/(s^3). Where is the missing acceleration component (m/s^2) in the rolling resistance equation?
I found the same. The units in the rolling resistance are ( kg*m/s), whereas the units of power (watts) are kg*m^2)/(s^3). An acceleration value (m/s^2) is needed. g would make sense as the rolling resistance needs the force the rider + bike imparts to the road – i.e. mass * g. This would mean multiplying the rolling resistance by 9.8 .
Your equation states: Power required to overcome rolling resistance, P = krMs. How does kg*(m/s) = Watts? There’s a missing acceleration component (m/s^2).
That first photo. You could at least get the horizon horizontal.
What I was trying to figure out on the bike today is what the delta (change) in effort (watts) expressed as a percentage for every addition 1% of grade. I’m too tired from my bike ride up a 10 mile hill at the moment to be certain your formula could be used to get the answer to the problem I pose. Maybe you have thought of it. What I might do is plug your formula into a spreadsheet and vary the grade, and take the difference in wattage. Sounds simple enough, but I don’t think I could have done what you have here. Very good and helpful. Thanks!
I am super impressed by your fun and knowledgeable approach to informing those of us who are obsessed with this kind of stuff. Just finished going over the North Cascades Highway in Washington state. Having done a few epic bike rides, this route is about as spectacular as it gets. The gradient is just shy of 10%. 5100′ in 57 miles. The scenery is truly amazing. Encountered maybe 20 other cyclists throughout the day enjoying this incredible experience. Highly recommended. Cheers from Washington state.
5100 feet in 57 miles is 1.6%, not 10%
Please!
I need a help from anyone using this bike tool.
I am writing a thesis about sloping down with a bicycle and I need the minimum slope gradient that the bike stay running in the constant velocity.. no accelerations.. without the cyclist force…
I´ve watching some results and it may be in -1% or less.. (I hope -0,5%)
I need the grade the bike stay at the same velocity all the 186 m constant slope.
Please send me your results to fadul@poli.ufrj.br or my whatsapp phone number +5521987672152
Thanks a lot!
You will help to build some good things to bicycle technology.
Marcelo.
My favorite part was the diagram which uses as an example, Rider + Bike = 85kg.
I wish.
There’s an interesting way to apply this to longer rides with a lot of climbing such as the Three Peaks. If the total ascent is 4000m, and the weight of the bike and rider is 90kg (I wish!), then a total of 4000 x 9.8 x 90 = 3,528,000 Joules needs to be found just to lift the weight up that distance. At a sustained output of 200W (200 Joules/sec) it would need 4.9 hours just to provide that energy. Add rolling resistance and air resistance…
According to research it appears that above 20% gradient you’re better off walking on a metabolic efficiency point of view. The point of dispute though is whether to carry or to push the bike under those conditions.
Wow!
You guys are thorough bike nerds. I love it.
Hi,
I really like your analysis of power and climbing. I wish I was as mathematically adept. I have been trying to find a way of calculating the optimal gear for a given power to weight output and cadence. Specifically I am doing the Haute route Alps in August and want to be able to ride as efficiently as possible over successive days.
Thanks,
Niall
Power = Work / Time = Force * Displacement / Time = (Mass * Acceleration *Displacement) / Time
hence Power-to-wheight depends quadratically on Mass !
Nice article, mate.
I found your blog googling about Alto de Letras.
I have a question. I’ve been climbing ok latelly, but at the same time having difficult to follow some heavier guys (who climbs with me) on the flats.
I never tought this, but can I assume that wind resistance much higher at higher speeds is one of the main reasons? Or is just a matter of improve power outputs?
Thank you and congratz.
Very nice blog.
Hi Fabio, this might be of interest: http://cyclingtips.com.au/2013/09/climbing-and-time-trialling-how-power-outputs-are-affected/
Cheers!
Wow. Nailed it!
Perfect!
Thank you very much.
So… At 114kg in underwear first thing in the morning, lets say 116kg after a meal and wearing my cycle clothes…. plus my bike is around 11kg including pump/spare tyres etc…
So we’re talking around a total weight of 127kg to get up the hill, I don’t feel quite so bad about taking 27 minutes to get up the 1:20 now!
Yes that is all very well that a lighter rider can ride up hills faster than a heavy rider assuming they ( the lighter rider) have a higher power to weight ratio. But this is not the case a heavy rider:
1) can produce more power,
2) has a higher power to total weight ratio (bike weight included)
3) can ride faster on the flat and on negative grades
please explain,
Good one, big like
Thanks so much for your great analysis Matt.
1kW to do those 20% gradients is A LOT!
I reckon that if there is no wind ka (wind resistance coefficient) should be 1.0. If there is a head wind, this number will be greater than 1.0. If there is a tail wind, this number will be less than 0. I’d suggest 0.5 would be a fairly strong tailwind!
Awesome article Matt!
Less time at the pie shop for me now…
A truly rewarding article Matt. I appreciate the extent of research you’ve done for this.
A related topic I’ve been wanting to satisfy is that of Energy Expended. The Garmin Edge will produce an estimate of this parameter and Strava will also. Disappointingly the two estimates are wildly different for the same data set. So the algorithm that each company uses is certainly quite different. The reason for my interest is in order to correlate the energy expended during my own endurance rides with trips I’d like to do. Some trip data of yours and Wades for endurance trips we can see online as Strava reports however they cannot be compared with Garmin reports. Cheers.
Thanks very much Trevor! I’ll definitely look into the energy expenditure issue. 🙂
If you have a power meter then it is simple: energy expended = average power (W) * time riding * human metabolic efficiency factor (which I personally just assume is 4). For example, today I did Frankston & back at a gentle pace, averaging 191W for the 2h45m. Total energy expended? Find out here: http://goo.gl/ZUNu5
For those without a power meter, the estimation is based on heart rate. I usually find Strava’s estimates, which are based on their power estimates, to be substantially over the real energy expenditure (especially for bunch rides); Garmin Connect, which I believe uses the Firstbeat algorithm, comes closer. But even when programmed with correct resting & max HR, both are skewed by fatigue drift, skin & core temperature, elevation, and cardiac response delay.
that must be a really heavy bike Matt 🙂 Thanks for these posts.
Well, let’s say you’ve got a bike that in race configuration is a UCI legal 6.8kg. Swapping out for the training wheels, Ultegra cassette, all-day tough tyres, two bidons of water, saddlebag, tube, tookit, lights, frame pump and it’ll quickly gain weight! 10kg is not an unreasonable estimate for training calculations.
I was guessing the other way i.e. your weight to be around 70kilos.
My bike is 13-14kg anyways.
Ha, no, try 80kg.
so you’re saying you weigh 90kg with your bike?
Yes indeed.
This article is a masterpiece. Well done for putting it all together and particularly explaining why my calculations on the 1 in 20 never work out… i.e. extra wind resistance in the false flat.
It’s this dedication of yours that rewarded you with some huge PBs recently.
I’m amazed that you don’t ride with a power meter!
So what’s the plan to crack 17 minutes on the 1 in 20?
Thanks James. According to the Bike Calculator app I’d need to lose 5kg in order to go under 17 minutes. 😉
Or, alternatively, do a few more ascents of Kinglake to push up those wattage numbers. Hope you didn’t get rained on.
Interesting stuff. I think (just intuitively) that the windspeed signs might be mixed up.
v = speed of the bike through the air (i.e. bike speed – headwind or + tailwind)
should probably be
v = speed of the bike through the air (i.e. bike speed + headwind or – tailwind)
Yep, good point. I’ll fix that up.
Given I need to add the weight of my bike to the your total weight… the key take home message from all of this is “stop eating cake” (and yes I already knew this, but you had to go and quantify the impact didn’t you)
Another great article Matt,
I know the the maths makes perfect sense, but why does a steeper hill feel like it takes SO MUCH MORE effort?
Not having a power meter probably has something to do with the feeling I’m working harder for less output!
simply that we choose to work harder on steep grades. we don’t need to, we could select and/or fit a sufficiently low gear to cruise up gently, but it’s like when you’re walking along gently and you encounter some steps – natural instinct is to attack them.
The answer here is gravity. The giMs part of the equation. The power required just to go nowhere.
Now the maths here is an approximation that works rather well until you hit super steep roads (that just don’t exist)
On a flat surface the power to overcome gravity is zero.
On a 10% gradient that is equal to 9.8 x .10 x your body mass. So that is (using the 90kg example) 9.8*.1 *90 = 88.2 Watts taken just to go nowhere!
On a 20% climb it’s 176.4 Watts.
If you are a bike rider capable of producing consistantly in the order of 250-300 Watts it means that most of your effort is being used just to overcome your own (and your bikes) weight!
Plus you also wobble a fair bit when it gets super steep, the riding position isn’t comfortable and you have to expend energy to stop the front wheel from lifting and the back to have enough grip to stop spinning…
This also explains why descending is fun!
Sorry Dave, but I think you have misunderstood the equation. You can’t just discount the speed term in that equation and regard it as calculating the same thing. The 88.2 that you have calculated is actually the WORK required to lift your mass 10cm (or move up the 10% gradient one metre). POWER is time specific so you need to divide through by a time term (i.e. seconds) which is where the speed term comes in (i.e. metres/second, the distance from the speed multiplied by the gradient gives a vertical distance, the seconds makes it into a vertical distance per second). Therefore, 88.2 Watts is the amount of power required to move up a 10% gradient at 1m/s (3.6km/hr) discounting rolling friction and air resistance, NOT the power taken to go nowhere (this would be zero as the speed of going nowhere is 0 m/s). This is that same amount of power needed to lift 90kg at a speed of 10cm/second no matter what the method of propulsion (crane, bike on hill, running up stairs, etc).
To answer Nick O’s question it is simply a matter of efficiency. Road bikes are not optimised for riding up 20% gradients because the gears are generally too high and they’re hard to ride at slow speeds (lower than 10km/hr). Riding a mountain bike up a 20% gradient is easier because you can select a more appropriate gear and ride at a more sustainable (slower) speed and whilst still be ascending vertically at a similar rate. Interestingly, steeper climbs are actually more efficient when considering vertical height gain due to the reduced air and tyre resistance at lower speeds. Also, as Jules alluded to, there is a Psychological side to is as well.
Awesome article. Love it.
Does anyone have that all ready to go in a spreadsheet? Save me building one.
great article Matt. i find this stuff really interesting. i was fiddling around with this formula during the mountain time trial of the Giro recently, and it seems to be pretty accurate, in terms of producing the types of power figures as reported by riders themselves from their power meters.
the other measure i like to reference when assessing climbing performance is VAM, or rate of vertical ascent (the principle is dead simple, but its use was pioneered by none other than Dr Michele Ferrari). strava will produce this for you – although the error margin is inversely proportional to the length of the climb, i.e. inaccurate for short climbs.